Nous contacter

Quelques définitions :

	Période
	La période d'un signal correspond à l'intervalle de temps qui s'écoule entre deux passages successifs par le même état d'un phénomène périodique. La période d'un signal périodique est égale à l'inverse de la fréquence : T=1/f
	Fréquence
	Elle correspond au nombre de répétitions d'un phénomène périodique dans une unité de temps. Son unité est le Hertz (nb de répétitions par seconde). La fréquence d'un signal périodique est égale à l'inverse de la période: f=1/T
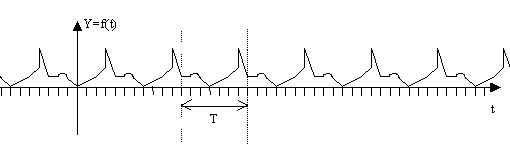
	Signal périodique
	Un signal périodique est un signal qui reprend la même valeur au bout d'un intervalle de temps régulier. Ainsi, une fonction périodique f de période T est telle que f (t+T)=f(t). Plus simplement, la représentation d'un signal périodique est un "dessin" répété tous les intervalles de temps T.
	Intégrale
	L'intégrale d'une fonction est définie sur un intervalle [a,b]. Son résultat représente l'aire comprise entre la courbe représentative de la fonction f et l'axe des abscisses. Elle se note de la façon suivante : 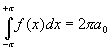Cette intégrale calcule l'aire comprise entre l'axe des abscisses et la fonction f(x) sur l'intervalle (en abscisse) [-pi,+pi].
	Fonctions paires
	Une fonction paire est une fonction qui prend la même valeur pour deux valeurs opposées de la variable. En d'autres termes, une fonction paire est telle que f(-x)=f(x) et sa courbe représentative est symétrique par rapport à l'axe des ordonnées.
	Fonctions impaires
	Une fonction impaire est une fonction qui change de signe en même temps que la variable. En d'autres termes, une fonction impaire est telle que f(-x)=-f(x) et sa courbe représentative est symétrique par rapport à l'origine O(0,0) du repère.
	Pulsation
	La pulsation d'un phénomène sinusoïdal est le produit de la fréquence f de ce phénomène par le facteur 2pi soit : w=2pi*f.