Les séries de Fourier
Une série de Fourier s'écrit sous la forme suivante :
son terme général est donc: 
et dépend d'une variable réelle x.
Remarque :
La périodicité de cos(nx) et de sin(nx) permet d'affirmer
que la série de Fourier écrite ici est périodique de période 2pi.
Si on suppose qu'une fonction f(x) peut être développée en une série de Fourier (de
terme général 
)on
recherche alors tous les coefficients a0, b0, a1, b1, a2, b2, … de cette série.
Calcul des coefficients de la série de Fourier :
Connaissant la fonction f(x), on veut la développer en une série de Fourier :
Pour cela on doit encore calculer les an à partir de f(x) et les bn à partir de f(x).
Premier terme a0 :
Réalisons une opération d'intégration (sur une période 2pi) sur chaque terme de l'égalité, on conserve l'égalité :
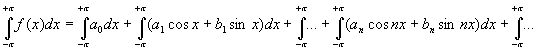
Or de tous les termes qui se trouvent à droite de l'égalité, seul le premier n'est pas nul (périodicité des cos et des sin). Il vient donc immédiatement que :
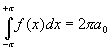
ce qui permet de dire que le terme a0 du développement en série de Fourier de f(x) est calculable à partir de la relation suivante:
Les coefficients suivants an et bn :
Multiplions de part et d'autre de l'égalité par cos(px) (p étant un entier non nul), on conserve toujours l'égalité:
Réalisons une opération d'intégration (sur une période 2pi) sur chaque terme de l'égalité, on conserve l'égalité :
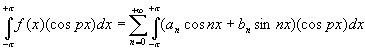
3 cas se présentent maintenant:
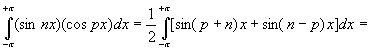
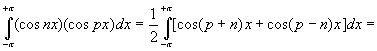
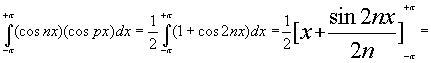
de même chaque terme bn du développement en série de Fourier de f(x) est calculable à partir de la relation suivante:
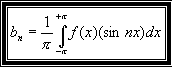
Conclusion fondamentale:
(Sous certaines conditions mathématiques toujours vérifiées dans le domaine du signal) Toute fonction f (de R dans R) périodique de période 2pi, et intégrable sur la largeur d'une période est décomposable en une série de Fourier. Cette décomposition s'écrit de la manière suivante :
Remarques :
- Si la fonction f(x) est PAIRE, son écriture en série de
Fourier n'y change rien et est elle aussi PAIRE. On en déduit qu'elle n'est composée que
des termes an et
(les termes 
étant eux impairs).
Donc:
1. tous les coefficients bn sont nuls.
2. Et pour
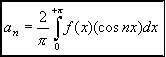(à démontrer).
- Si la fonction f(x) est IMPAIRE, son écriture en
série de Fourier n'y change rien et est elle aussi IMPAIRE.Cette fois on en déduit
qu'elle n'est composée que des termes 
(les termes a0 et 
étant eux pairs).
Donc:
1. Tous les coefficients an sont nuls y compris a0.
2. Et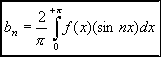 
(à
démontrer).
- Dans le calcul des coefficients de la série de Fourier l'opération d'intégration a été réalisée de -pi à +pi. Elle aurait pu être faite entre n'importe quelles bornes séparées de 2pi radians, l'important étant de la réaliser sur une période entière de la fonction f(x).
Cas d'une fonction de t, périodique de période T:
Une fonction du temps f(t) est périodique de période T, si elle est représentée par un motif de durée T qui se répète indéfiniment. La représentation graphique de f(t) peut avoir l'allure suivante par exemple:
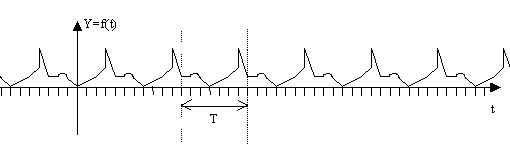
La fonction f(t) peut être réécrite en fonction de x (en radians) et s'appellera alors g(x) de période 2pi (radians). Le graphe de g(x) est le même que celui de f(t) mais représenté en fonction de la variable x et non plus t.
Dans le changement de variable on est passé de t à x et de T à 2pi. L'équation de changement de variable s'écrit donc :
et on notera : 
.
Compte tenu de cette relation entre x et t, la fonction g(x) n'est qu'une écriture différente de la fonction f(t), on a donc l'égalité suivante:
ou 
.
Puisqu'on cherche la série de Fourier de f(t), écrivons d'abord celle de g(x), on en déduira bien celle de f(t).
avec pour coefficients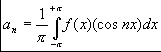 
et 
Ecrivons la en fonction de 
:
Donc la série de Fourier de f(t) s'écrit de la façon suivante:
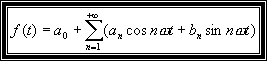
les coefficients deviennent :
 |
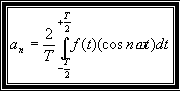et |
 à
démontrer |
et  |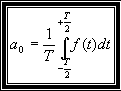
à démontrer |
Exemple : Fonction triangulaire
Forme complexe de la série de Fourier d'une fonction f(t) de période T :
Le terme général de la série de Fourier de f(t) s'écrit à l'aide d'une fonction SINUS et d'une fonction COSINUS :
Nous savons d'après le chapitre sur les nombres complexes (voir les formules d'Euler), qu'on peut écrire un SINUS ou un COSINUS à partir d'un complexe et de son conjugué :
Rappels :
et 
Cas du terme général de la série:
En utilisant les formules d'Euler, on peut écrire le terme général à l'aide des nombres complexes :
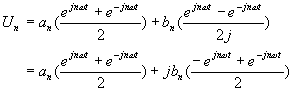
Après mise en facteur de 
d'une part et de 
d'autre part, on obtient:
On remarque que a(-n)=an et b(-n)=-bn.
On peut donc écrire :
avec 
et 
En calculant Cn, on trouve son expression :
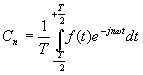
Cas du terme a0 :
Si dans l'expression de Cn, on applique n=0, on aboutit à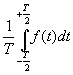 
c'est à dire a0. Donc l'expression général de
Cn est vraie aussi pour le terme a0.
Conclusion :
La forme complexe de la série de Fourier de la fonction f(t) périodique de période T s'écrit :
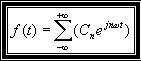
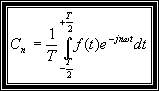
Analyse harmonique:
Une fonction périodique f(t) quelconque est développable suivant la série de Fourier suivante :
Le terme général de la série, 
peut s'écrire avec la factorisation suivante:
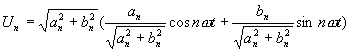
on peut vérifier le résultat suivant:
qui nous permet de poser:
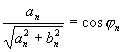et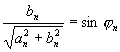 
L'expression de
devient
alors:
et s'écrit aussi:
où 
et 
.L'angle jn, introduit
ci-dessus est donc le déphasage du terme général.
Ainsi toute fonction périodique f(t) quelconque se développe en une série de Fourier qui peut aussi s'écrire :
avec 
et 
la fonction f(t) apparaît donc comme la somme :
- d'un terme constant a0 qui représente la valeur moyenne de f sur une période T
- d'une infinité de fonctions sinusoïdales de pulsations w, 2w, 3w, …(, nw…) et d'amplitudes A1, A2, A3, …(, An…) avec chacune son propre déphasage j1, j2, j3, …(,jn…). La fonction sinusoïdale de période T (pulsation w) est appelée le fondamental. Les suivantes (de périodes T/2, T/3, T/4, … ou de pulsations 2w, 3w, 4w, …) sont appelées les harmoniques de rang n.